정렬 알고리즘이란?

정렬 알고리즘은 목록의 요소들을 순서대로 넣는 알고리즘이다. -위키백과

정렬을 해야하는 이유?

데이터를 정렬해야 하는 이유는 탐색을 위해서이다. 사람은 수십에서 수백 개의 데이터를 다루는 데 그치지만 컴퓨터가 다뤄야 할 데이터는 보통이 백만 개 단위이며 데이터베이스 같은 경우 이론상 무한 개의 데이터를 다룰 수 있어야 한다. 데이터가 정렬되어 있다면 효율적으로 정보를 탐색할 수 있다. -나무위키

시작하기 전에..

정렬의 종류가 다양한 이유

  1. 정렬 방법의 따라 시간복잡도가 다르다.
  2. 정렬 방법의 따라 공간복잡도가 다르다.
  3. Stable/unstable한 정렬의 필요성. -임베디드 블로그
  • 정렬들을 위 3가지 항목을 이용해 평가 하도록 하겠습니다.

평가 항목

  1. ⏱ 시간 복잡도
    • 연산을 완료하는데 걸리는 시간.
  2. 💾 공간 복잡도
    • 연산을 완료하는데 필요한 정장공간.
  3. 🗻 Stable vs 🌋 Unstable
    • 같은 값을 가진 node들이 정렬 전후에 순서가 변경 되었을 경우 unstable.
    • 순서가 유지되었으면 stable.

빅오 - Big O

🎯 빅오는 무엇인가?

  • 시간 복잡도와 공간 복잡도를 표기할때 사용하는 기호다.
  • 연산 횟수에 비해 시간/공간의 증가를 측정.

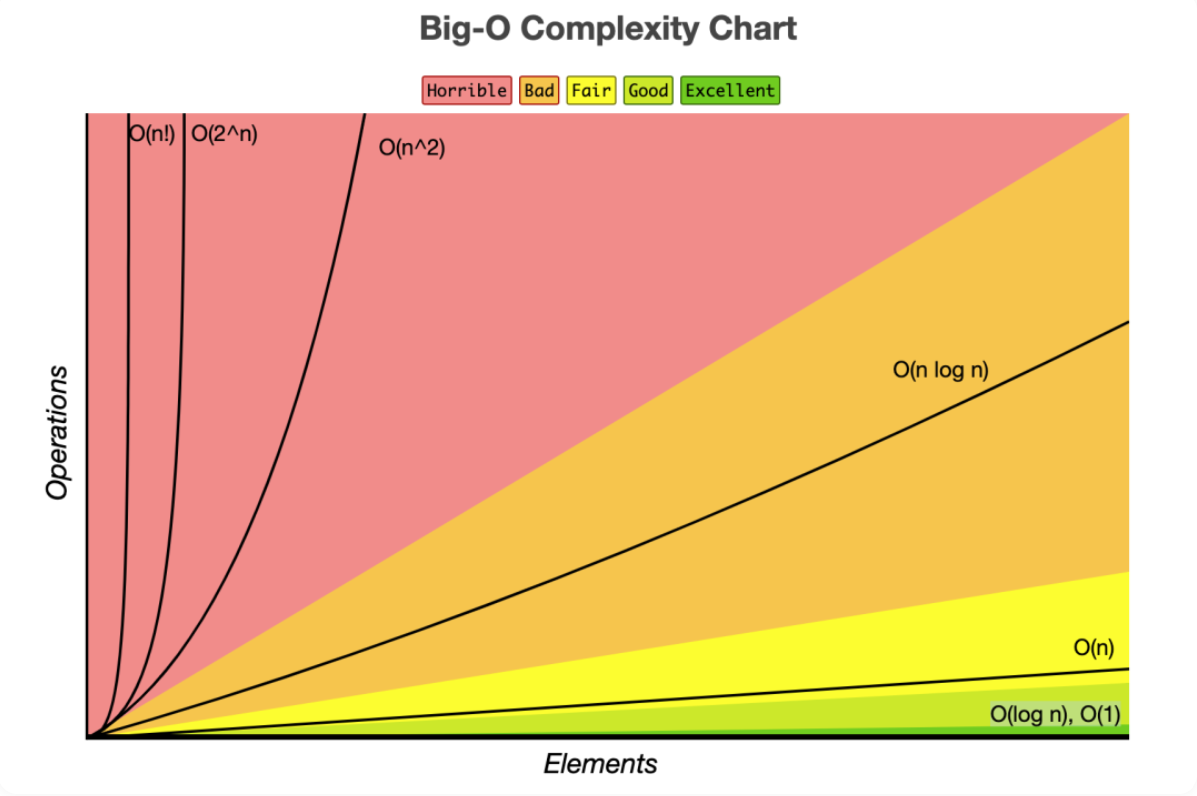
종류(작은 순):

  • O(1)
  • O($log$ n)
  • O(n)
  • O(n $log$ n)
  • O(n$^2$)
  • O(n$^3$)
  • O(2$^n$)

정렬의 종류

📌 Bubble Sort(거품 정렬)

  • 인접 node가 잘못된 순서일 경우 해당 node를 반복적으로 교환하여 정렬합니다.

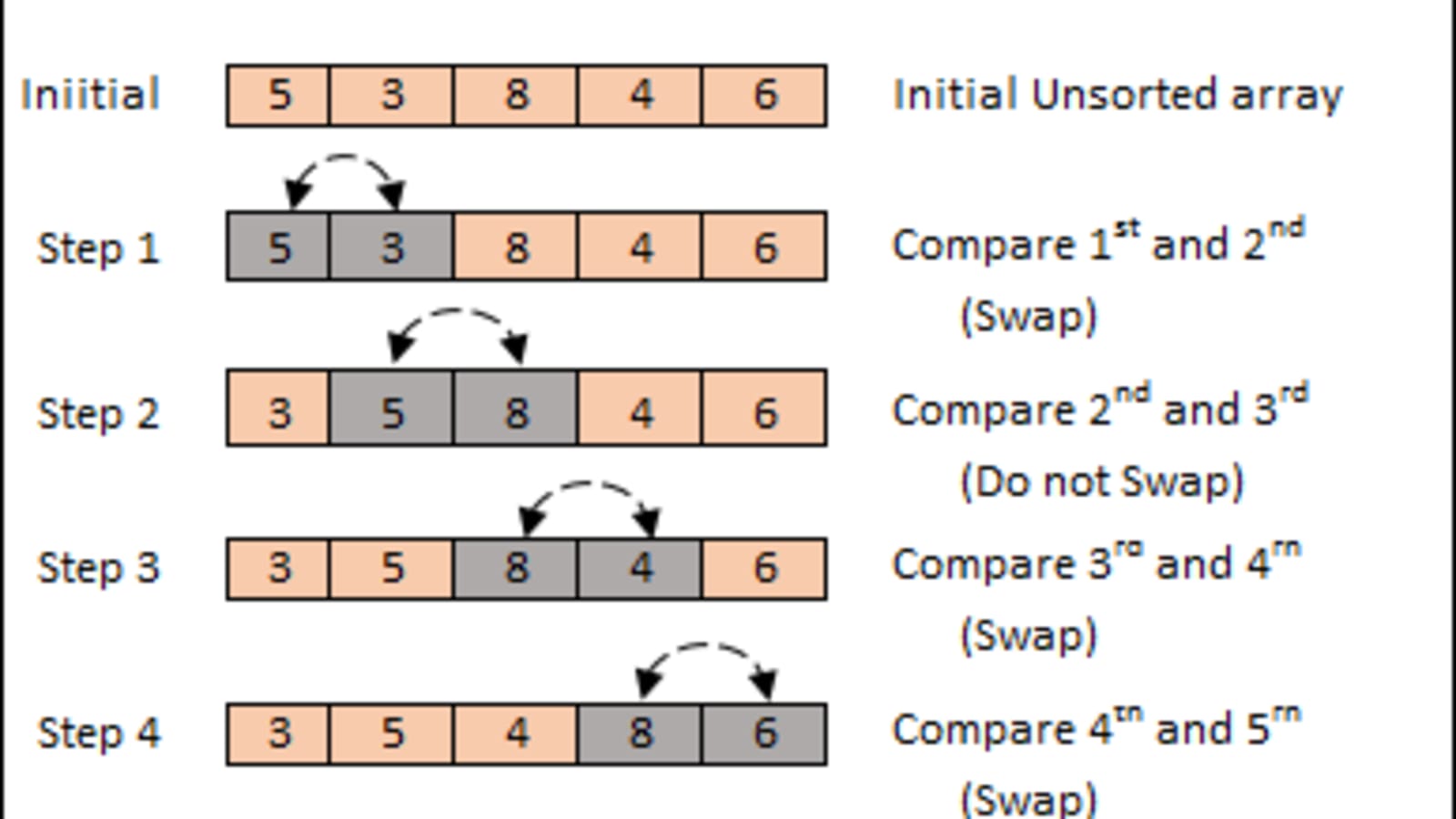
array arr[] = {5, 1, 4, 2, 8}

❗ 노랑: 비교되는 node

1st pass:

{5 1 4 2 8} -> {1 5 4 2 8} //5 > 1, 교환. {1 5 4 2 8} -> {1 4 5 2 8} //5 > 4, 교환. {1 4 5 2 8} -> {1 4 2 5 8} //5 > 2, 교환. {1 4 2 5 8} -> {1 4 2 5 8} //5 < 8 교환 하지 않음.

arr[] == {1 4 2 5 8}

2nd pass:

{1 4 2 5 8} -> {1 4 2 5 8} {1 4 2 5 8} -> {1 2 4 5 8} //4 > 2, 교환. {1 2 4 5 8} -> {1 2 4 5 8} {1 2 4 5 8} -> {1 2 4 5 8}

arr[] == {1 2 4 5 8}

3rd pass:

{1 2 4 5 8} -> {1 2 4 5 8} {1 2 4 5 8} -> {1 2 4 5 8} {1 2 4 5 8} -> {1 2 4 5 8} {1 2 4 5 8} -> {1 2 4 5 8}

arr[] == {1 2 4 5 8}

🎯 정렬이 되어있지만 교환 없이 처음부터 끝까지 통과해야 정렬되었음을 알 수 있음. 👍 정렬 중 가장 심플하다. 👎 시간 복잡도가 아주 높아 대량의 데이터를 정렬하기 적합하지 않다.

💯평가  
시간 복잡도 O(n$^2$)
공간 복잡도 O(1)
Stable vs Unstable Stable

📌 Insertion Sort(삽입 정렬)

  • 모든 node를 앞에서부터 차례대로 비교하여 자기 위치에 삽입하여 정렬합니다.
    • 손안의 카드를 정렬하는 방법과 유사해서 직관적이다.
    • Key node를 설정해 삽입한다.
      • Key값은 배열의 순서에서 한칸씩 증가.

array arr[] = {5, 1, 4, 2, 8}

❗ 노랑: 비교되는 node

1st pass (Key: 1):

{5 1 4 2 8} -> {1 5 4 2 8} //5 > 1, 5자리에 1 삽입.

arr[] == {1 5 4 2 8}

2nd pass (Key: 4):

{1 5 4 2 8} -> {1 4 5 2 8} //5 > 4, 교환. {1 4 5 2 8} -> {1 4 5 2 8} //1 < 4, 5자리에 4 삽입.

arr[] == {1 4 5 2 8}

3rd pass (Key: 2):

{1 4 5 2 8} -> {1 4 2 5 8} //5 > 2, 교환. {1 4 2 5 8} -> {1 2 4 5 8} //4 > 2, 교환. {1 2 4 5 8} -> {1 2 4 5 8} //1 < 2, 4자리에 2삽입.

… arr[] == {1 2 4 5 8}

🎯 삽입될 위치를 찾고 기존 자리까지 존재하는 node들이 한칸씩 뒤로 이동됨. 👍 정렬 중 가장 직관적이다. 👎 시간 복잡도가 아주 높아 대량의 데이터를 정렬하기 적합하지 않다.

💯평가  
시간 복잡도 O(n$^2$)
공간 복잡도 O(1)
Stable vs Unstable Stable

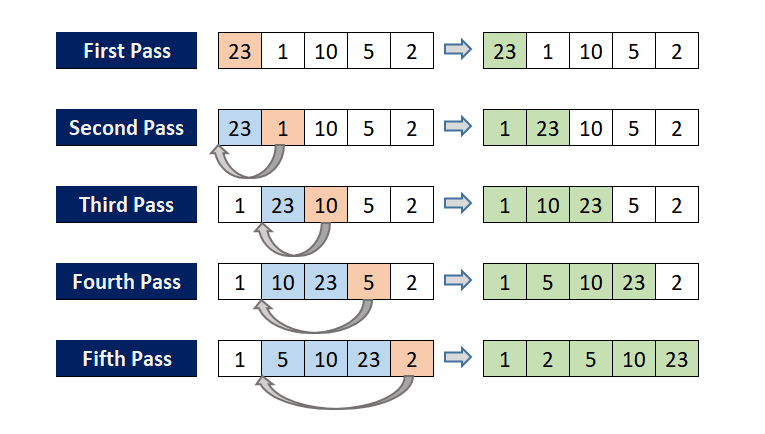
📌 Selection Sort(선택 정렬)

  • 가장 작은 node를 선택해 맨 앞으로 이동한다.
    • 앞에서 순차적으로 정렬된 배열에 추가한다.

array arr[] = {5, 1, 4, 2, 8}

❗ 노랑: 정렬된 배열

1st pass:

{5 1 4 2 8} -> {1 5 4 2 8} //1, 5와 교환.

arr[] == {1 5 4 2 8}

2nd pass:

{1 5 4 2 8} -> {1 2 4 5 8} //2, 5와 교환.

… arr[] == {1 2 4 5 8}

🎯 각 pass마다 가장 작은 값이 맨앞에 오게 되는 과정을 반복한다. 👍 직관적이고 심플하다. 👎 Unstable한 정렬이다.

💯평가  
시간 복잡도 O(n$^2$)
공간 복잡도 O(1)
Stable vs Unstable Unstable
  • Unstable한 이유:
    • arr[] == {5(a) 2 9 5(b) 4 3 1 6}
    • 가장 작은 수 인 1을 첫 node인 5(a)를 교환.
    • arr[] = {1 2 9 5(b) 4 3 5(a) 6}
    • 같은 값을 가진 node들의 순서가 바뀌었다.

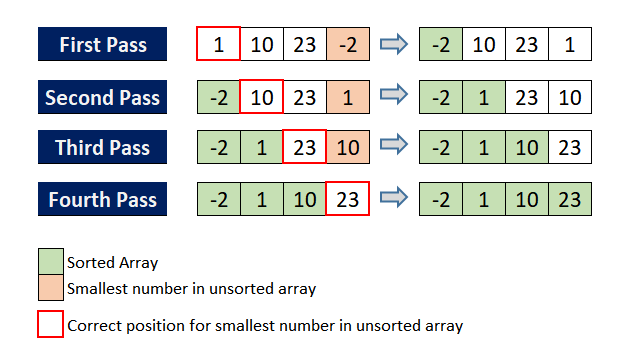
📌 Quick Sort(퀵 정렬)

  • 분할정복 (divide and conquer)전략.
    • 배열을 분리해서 졍렬 후 합쳐서 정렬한다.
      • 피벗 (pivot)을 기준삼아 작은 값들은 왼쪽으로 큰 값들은 오른쪽으로 이동 시킨다.
      • 피벗을 제외한 왼쪽/오른쪽 배열을 같은 방법으로 정렬한다.
  • 정렬하는 단계:
    1. low와 high 포인터를 정해준다.
      • arr[low]는 피봇보다 작아야함.
      • arr[high]는 피봇보다 커야함.
    2. low와 high 포인터가 서로 지나칠때까지 다음 작업을 반복:
      • low와 high 포인터들의 조건이 성사되지 않을 경우 서로 값을 교환.
    3. high포인터와 피봇을 교환.
    4. 피봇을 기준으로 왼쪽과 오른쪽 배열을 재귀로 반복.

array arr[] = {5, 1, 4, 6, 2, 8}

❗ 노랑: pivot ❗ 분홍: low ❗ 주황: high

1st pass (Pivot: 5):

{5 1 4 6 2 8} 1 < 5 ⭕ 8 > 5 ⭕

low, high 한칸씩 이동.

arr[] == {5 1 4 6 2 8}

2nd pass (Pivot: 5):

{5 1 4 6 2 8} 4 < 5 ⭕ 2 > 5 ❌

//high 정지.

{5 1 4 6 2 8} 6 < 5 ❌ 2 > 5 ❌

low와 high둘다 조건을 성사하지 못해 교환.

arr[] == {5 1 4 2 6 8}

3rd pass (Pivot: 5):

{5 1 4 2 6 8}

low와 high가 서로 지나침. 피봇과 high 교환.

{2 1 4 5 6 8}

피봇 (5)는 이미 정렬된 상태. 피봇의 왼쪽과 오른쪽을 같은 작업을 반복한다. (분할 정복)

  • {2 1 4} 5 {6 8}

정렬된 배열들은 결합한다. … arr[] == {1 2 4 5 6 8}

🎯 분할 (Divide)-> 정복 (Conquer)-> 결합 (Combine) 과정. 👍 정렬 중 속도가 빠른 편이다. 👍 추가 메모리 공간이 필요없다. 👎 이미 정렬된 리스트에 대해서는 수행시간이 더 걸린다.

💯평가  
시간 복잡도 O(n $log$ n)
공간 복잡도 O($log$ n)
Stable vs Unstable Unstable

📌 Merge Sort(합병 정렬)

  • 분할정복 (divide and conquer)전략.
    • 배열을 분리해서 졍렬 후 합쳐서 정렬한다.
      • 개념은 퀵 정렬과 비슷하다.
  • 정렬하는 단계:
    • 배열의 길이가 0 이거나 1이면 정렬된 것으로 간주한다.
      1. 배열을 반으로 분활한다.
      2. 나뉘어진 각 배열을 재귀적으로 정렬한다.
      3. 다시 하나로 합병한다.
      1. left는 왼쪽 배열의 가장 왼쪽 부터, right는 오른쪽 배열의 가장 왼쪽부터 시작.
      2. 서로 비교하여 정렬된 배열에 추가.
      3. 사용된 포인터 한칸 이동.

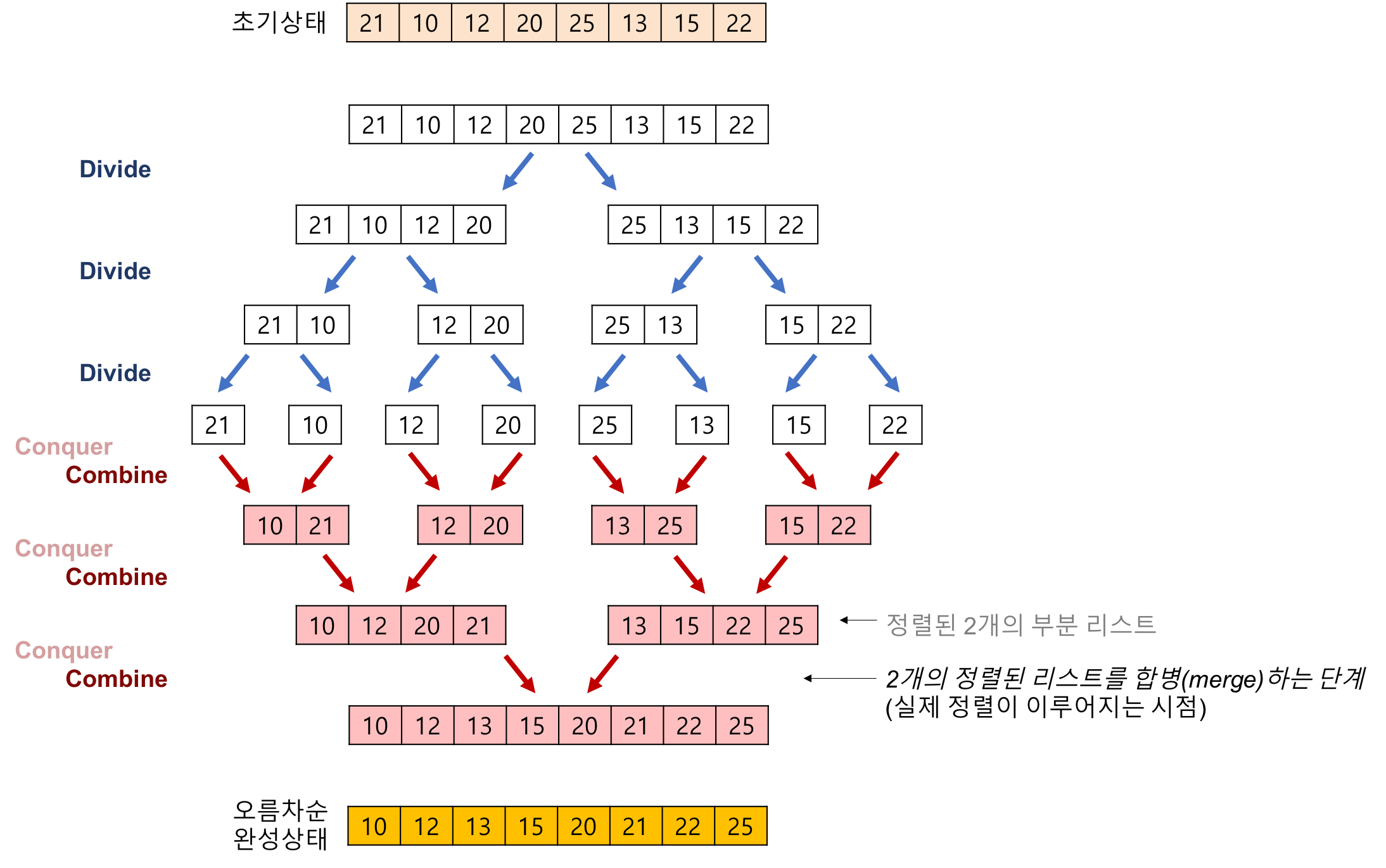
  • 합병하는 과정:

    array arr[] = {5 1 4 6 2 8}

    ❗ 노랑: left ❗ 분홍: right

    …(분할)

    {5} {1} {4} {6} {2} {8}

    …(합병)

    1st pass:

    {1 4 5} {2 6 8}

    sorted arr[] = {1}

    2nd pass:

    {1 4 5} {2 6 8}

    sorted arr[] = {1 2}

    3rd pass:

    {1 4 5} {2 6 8}

    sorted arr[] = {1 2 4}

    4th pass:

    {1 4 5} {2 6 8}

    sorted arr[] = {1 2 4 5}

    5th pass:

    {1 4 5} {2 6 8} //둘중 하나가 먼저 끝나면 나머지 값들을 전부 복사한다.

    sorted arr[] = {1 2 4 5 6 8}

🎯 분할 (Divide)-> 정복 (Conquer)-> 결합 (Combine) 과정. 👍 정렬 중 속도가 빠르고, 효율적인 편이다. 👎 초보자가 구현하기에 복잡하다.

💯평가  
시간 복잡도 O(n $log$ n)
공간 복잡도 O(n)
Stable vs Unstable Stable

출처

[위키백과] (https://en.wikipedia.org/wiki/Sorting_algorithm) [나무위키] (https://namu.wiki/w/%EC%A0%95%EB%A0%AC%20%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98) [임베디드 블로그] (https://noel-embedded.tistory.com/1095)